Should you keep the first Envelope or change? Choice between “Two Envelopes Paradox”

You are offered a choice between two envelopes E1 and E2. All that you know about them is that one contains twice as much money as the other. After you have chosen one of the envelopes, you are offered the opportunity to switch the envelope that you have chosen for the other envelope.

Should you keep the first Envelope or change?

Moreover—since your choice between the two envelopes was undertaken in complete ignorance of the contents of the two envelopes—you should regard the two possible outcomes as equally likely.

0.5×$2x+0.5×$0.5x=$1.25x

Since the expected utility of trading E1 for E2 is greater than the expected utility of hanging on to E1, you should switch. (1.25 is greater than 1.0 … RIGHT????)

you should switch. 1.25 is greater than 1.0 … RIGHT????

To find out write for the amount that’s in your chosen envelope. This means that the amount of money in the other envelope is eithe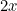r or 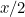. The probability that it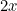’s is 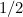and so is the probability that it’s 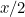. So the expected amount you’ll get for switching is

Since that’s bigger than , you should swap envelopes. But what if you are given another chance to swap envelopes after you have changed your mind once? By the same reasoning as above you should swap back again. And then, by the same argument again, you should swap a third time, and so on, forever. You end up in an infinite loop of swapping and never get any money at all. What’s wrong with this reasoning?

A resolution

Let’s write 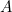for the envelope you picked at first and for the other one. We write for the amount of money in 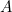. Now since we haven’t opened envelop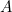e , isn’t a fixed amount: it’s a random variable. It can take one of two values: the smaller amount of money that’s hidden in the two envelopes or the larger amount of money. Let’s write 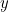for the smaller amount and 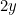for the larger amount (recall that one envelope contains twice as much money as the other). Since you have picked 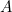randomly, there’s a 50:50 chance that 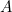contains either of the two amounts. This means that the expected amount of money 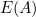in envelope 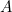is

We said above that the expected amount in envelope is

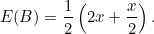
(1)

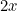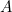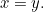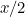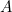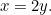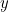But recall that isn’t a fixed amount but can take one of two values. In the case that envelope contains , envelope contains the smaller amount of money, so In the case that envelope contains , envelope contains the larger amount of money, so So in formula (1) above, the first really stands for and the second stands for 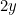. The two 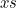in the formula are actually different and shouldn’t have been added up to give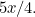

Substituting the 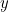for the first appearance of in (1) and 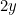for the second gives

Thus 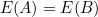so there is no incentive to switch envelopes and hence no paradox.